37. Mail of the sponsor

You remember the problem “The word of sponsor” from New Year contest. I remind you briefly that problem: after the event finished, the sponsor wanted to send out the prizes for winners.

But the postal system is not perfect and not all the prizes can be delivered to participants. There are n post offices in the country, numbered from 1 to n. The sponsor sends the prizes from the office number s. Also, we know the mail transportation system – the pairs of post offices between which the mail can be passed.

Before the new competition the sponsor decided to guarantee the safe delivery of prizes. To do this, the sponsor is ready to establish new links between some pairs of post offices. Your task is to find the least amount of new connections, so that prizes can be delivered after the competition to all participants, regardless of where they live and which post office use.

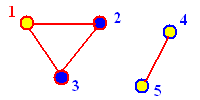
Input. First line contains three integers – the number of post offices n (1 ≤ n ≤ 10⁵), the number of post office the sponsor uses s (1 ≤ s ≤ n) and the number of links between the pairs of offices k (0 ≤ k ≤ 10⁵).

Each of the next k lines contains 2 numbers: a and b – the numbers of post offices, between which the mail transportation exists (a and b are different numbers from interval [1; n]). All the pairs (a, b) are different.

Output. Print one number – the minimum possible number of new connections to be created, so that the mail can be delivered from s to any other post office.

Sample input	Sample output
5 1 4 1 2 2 3 1 3 4 5	1

SOLUTION

disjoint set

Algorithm analysis

The number of new connections equals to the number of connected components of the graph minus 1. Since n ≤ 10⁵, to solve the problem we must use a system of disjoint sets with heuristics.

Algorithm realization

Declare the arrays.

vector<int> parent, depth;

Function Repr finds a representative of the set that owns the vertex v.

int Repr(int v)

{

if (v == parent[v]) return v;

return parent[v] = Repr(parent[v]);

}

Function Union unites the sets with vertices x and y. A set with a lower height joins a set with a higher height.

void Union(int x, int y)

{

x = Repr(x), y = Repr(y);

if (x == y) return;

if (depth[x] < depth[y]) swap(x, y);

parent[y] = x;

if (depth[x] == depth[y]) depth[x]++;

}

The main part of the program. Read the input data. Initialize the arrays.

scanf("%d %d %d", &n, &s, &k);

parent.resize(n + 1);

depth.resize(n + 1);

for (i = 0; i <= n; i++) parent[i] = i;

Read the edges of the graph. Perform the Union operation on a pair of vertices of each edge.

for (i = 0; i < k; i++)

{

scanf("%d %d", &a, &b);

Union(a, b);

}

The number of sets equals to the number of connected components of the graph.

for (c = 0, i = 1; i <= n; i++)

if (parent[i] == i) c++;

Print the number of new connections that should be built.

printf("%d\n", c - 1);

Algorithm realization – classes

#include <cstdio>

#include <algorithm>

#include <vector>

using namespace std;

int i, n, s, k, a, b;

class dsu

{

public:

vector<int> parent, depth;

dsu(int n)

{

parent.resize(n + 1);

depth.resize(n + 1);

for (int i = 0; i <= n; i++)

parent[i] = i;

}

int Repr(int v)

{

if (v == parent[v]) return v;

return parent[v] = Repr(parent[v]);

}

void Union(int x, int y)

{

x = Repr(x), y = Repr(y);

if (x == y) return;

if (depth[x] < depth[y]) swap(x, y);

parent[y] = x;

if (depth[x] == depth[y]) depth[x]++;

}

int getSets()

{

int cnt = 0;

for (int i = 1; i <= n; i++)

if (parent[i] == i) cnt++;

return cnt;

}

};

int main(void)

{

scanf("%d %d %d", &n, &s, &k);

dsu ds(n);

for (i = 0; i < k; i++)

{

scanf("%d %d", &a, &b);

ds.Union(a, b);

}

printf("%d\n", ds.getSets() - 1);

return 0;

}

Java realization

import java.util.*;

public class Main

{

static int parent[], depth[];

static int Repr(int v)

{

if (v == parent[v]) return v;

return parent[v] = Repr(parent[v]);

}

static void Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return;

if (depth[x] < depth[y])

{

int temp = x; x = y; y = temp;

}

parent[y] = x;

if (depth[x] == depth[y]) depth[x]++;

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int s = con.nextInt();

int k = con.nextInt();

parent = new int[n+1];

depth = new int[n+1];

for(int i = 0; i <= n; i++) parent[i] = i;

for(int i = 0; i < k; i++)

{

int a = con.nextInt();

int b = con.nextInt();

Union(a,b);

}

int c = 0;

for(int i = 1; i <= n; i++)

if(parent[i] == i) c++;

System.out.println(c - 1);

con.close();

}

}

Java realization – classes

import java.util.*;

class dsu

{

int parent[], depth[];

public dsu(int n)

{

parent = new int[n + 1];

depth = new int[n + 1];

for (int i = 0; i <= n; i++)

parent[i] = i;

}

public int Repr(int v)

{

if (v == parent[v]) return v;

return parent[v] = Repr(parent[v]);

}

public void Union(int x, int y)

{

x = Repr(x); y = Repr(y);

if (x == y) return;

if (depth[x] < depth[y])

{

int temp = x; x = y; y = temp;

}

parent[y] = x;

if (depth[x] == depth[y]) depth[x]++;

}

public int getSets()

{

int cnt = 0;

for (int i = 1; i < parent.length; i++)

if (parent[i] == i) cnt++;

return cnt;

}

}

public class Main

{

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

int n = con.nextInt();

int s = con.nextInt();

int k = con.nextInt();

dsu ds = new dsu(n);

for(int i = 0; i < k; i++)

{

int a = con.nextInt();

int b = con.nextInt();

ds.Union(a,b);

}

System.out.println(ds.getSets() - 1);

con.close();

}

}